衝撃波の科学寄稿 高山 和喜 氏
第3回：衝撃波の数値模擬
2005/11中旬
19. 数値模擬（その２）
このノイマンパラドックスなる問題を、非粘性圧縮性流れを記述するオイラー方程式（Euler equations）ではなくて、くさび面に発達する境界層を記述できるナヴィヱ・ストークス方程式(Navier-Stokes equations)を差分法で解いて、数値計算で解決しようとした。しかし、1980年代、計算機の計算能力と記憶容量に限界があり、粘性計算と非粘性計算の結果には壁面付近にも大きな違いは認められなかった。ナヴィヱ・ストークス方程式を差分法で解いて、物理的に有意な結果を出すことがとんでもない大仕事になることは予測しなかった。
1994年、カナダのデユーイー教授は大きな衝撃波管でくさびを伝播する衝撃波の反射を多重露光撮影し、先端と後部で違った形態をとることに初めて気が付いた。この説明に、人々は実験の不備を指摘し、衝撃波が一定速度で伝播しないなどと批判し、誰もこの事実を認めなかった。1997年、オーストラリアのヘンダーソン教授はローレンスリバモア研究所のスーパーコンピューターを駆使して、この実験を再現した。計算格子を必要に応じて細分化し、境界層に６次の細分化を施して初めて数値解が収束した。計算は、膨大な計算量で、当時としては、気が遠くなるようなCPU時間を要した。
くさび先端で正常反射が現れて、ある距離伝播してマッハ反射が現れる事実が、初めて数値計算で再現できた。このとき、境界層を記述する格子の大きさは、実に、数ミクロンだった。くさび表面にはもっと大きな凹凸やさびが付着して数ミクロンの加工精度などありえない。でも、数値解は物理現象を再現した。要するに、ナヴィヱ・ストークス方程式が支配する世界と現実の物理現象は、この精度で対比しなければ現象を共有しないのだ。
我々は、自分の目で見てさわって確認しなければ、人の言うことを鵜呑みに信じないという愚者の誇りを持っている。素直に人の論文を信じる賢い人が多い。「万巻の書を読まば、書無きに似たり。」というように専門の論文を全て読んで信じれば、研究することも創造する必要もない。我々は、ヘンダーソン教授達の数値解に感心したが、素直に信じなかった。「数値計算は何でも作るから、これもその類ではないか。」と疑い、実験で定量的に追試しようと考えた。しかし、現存する衝撃波管の再現性は、目指す実験精度は保証されない。100mm×180mm衝撃波管を無隔膜仕様にして目標を満たす再現性を追求した。衝撃波管の再現性は重要である。
再現性が悪く衝撃波マッハ数がひどくばらついたとき、気に入ったデータだけを選んだらどうなるだろう。賢い研究者は同じことだと言うだろうが、理由を付けてデータ選別したら詐欺同然の処理になる。S字型に波打つ理論曲線があったとしよう。これに実験データ雲をかぶせて曲線に近いデータだけを残して他を消去し、消去したデータの範囲にエラーバーを付せば、道義責任を感じることなくデータ処理したことになる。
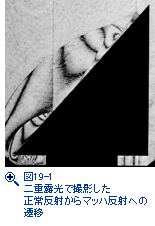
衝撃波管の再現性に注意を払うことなく多重露光撮影や高速映画撮影すれば、一回の実験でデータ取得可能になる。しかし、多重露光撮影や高速映画撮影画像の空間解像は非常に悪い。だから、衝撃波管の再現性に注意を払って、二重露光ホログラフィー干渉計で計測している。図19-1は衝撃波がくさび先端に到達した瞬間と後部に移動した瞬間の二重露光である。二回の露光の間に現れた、密度変化がそれぞれ干渉縞となって記録される。
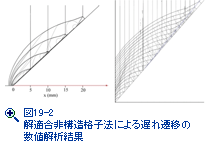2000年には、我々も自助努力で高次に格子を細分化できるようになり、境界層を解像して遅れ遷移を自由に数値模擬できるようになった（図19-2）。流体科学研究所にスーパーコンピューターが設置されて、大型計算が可能になった背景もあるが、数値計算のある概念が世に現れると忽ち普及する過程を目撃できた。特に、ローレンスリバモア研究所のパッケト博士とクラッチフィールド博士、マンチェスター大学のトロ教授、ロシア科学院ヨッフェ研究所のヴォイノヴィッチ博士、ヘブル大学のファルコヴィッチ教授、インド科学大学のカルカーニ博士に長期滞在して頂いて、絶えず刺激ある議論を通して我々の衝撃波数値模擬は進化したと考えている。また、同僚の齋藤務助教授（現在、室蘭工業大学教授）、バビンスキー博士（現在、ケンブリッジ大学助教授）、姜宗林助教授（現在、中国科学院力学研究所教授、高温物理研究室長）、エフゲニーチモフェエフ助教授（現在、マックギル大学助教授）、孫明宇助教授（現在、東北大学流体科学研究所）の研究が東北大学の衝撃波研究を支え、同時に、院生諸君を「門前小僧、習わぬ経を読む」の譬えのように、数値解析とコンピュータグラッフィクス研究の高見に導いた。
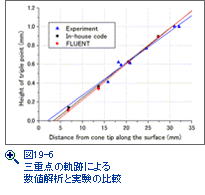
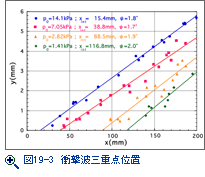ヘンダーソン教授の数値解は正しかった。図19-3はアルゴン中で衝撃波マッハ数2.327、くさび傾き角49°の実験で、縦軸はくさびに直交する距離、横軸はくさび面に沿う距離で、衝撃波三重点の位置を表示している。くさび先端近くでは、衝撃波三重点は現れず、ある点からマッハステムが発達する。マッハ反射は遅れて現れた。ヘンダーソン教授の数値解と実験結果を結ぶ直線はほぼ平行している。衝撃波管の側面壁影響で衝撃波は僅かに三次元的で、実験と数値解の差はこの影響である。
 |
|
 |
