HOME ＞ テクニカルレポート ＞ CAEと品質工学

CAEと品質工学寄稿　芝野 広志　氏　　高木 俊雄　氏　　平野 雅康　氏

実践編：CAEと品質工学を融合した事例

2005/09/05

5．ポイント3：実物再現性の確認
―直交表による交互作用の検査―

　 これまでに得られた結果が実物で再現するかどうか検査した。これは基礎編のポイント３で説明した直交表による制御因子間の交互作用の検査である。

　手順を簡単に説明する。

  1. 要因効果図から２つの制御因子の組み合わせ条件を決める。
  2. 最適条件を求める。
    「最適条件」は最もノイズによるバラツキが小さい条件で、要因効果図でＳＮ比の値が一番大きい制御因子の水準の組み合わせである。
  3. 最悪条件を求める。
    「最悪条件（現行条件でも良い）」はバラツキの大きい条件で、要因効果図でＳＮ比の値が一番小さい制御因子の水準の組み合わせである。
  4. 推定する。
    「推定」は、要因効果図を使って水準別の平均値から最適および最悪条件のＳＮ比を予測（推定）することである。言い換えると、この値は、制御因子間に交互作用が無かったと仮定したときの値である。
  5. 確認する。
    「確認」は、最適および最悪条件で表３のノイズを入れて、再び特性値をシミューションして、表４のデータを求めて、ＳＮ比を計算したものである。

表６　実物再現性の検査結果 [db]　推定と確認との結果を表６に示す。
　 表６より推定値と確認値の差(利得という)が１db以内で、推定値に対し確認値が高い再現性を持っていることがわかる。

図５　最適条件と最悪条件でのデータ　交互作用が無いと仮定して予測した推定値と実際にその条件でシミューションした値がほぼ一致すると言うことは、取り上げた制御因子間には交互作用が無いと言うことである。応用編で述べたように、取り上げた制御因子間に交互作用が無いと言うことは、取り上げていない他の制御因子間にも交互作用が無いと考えられる。
　 このことにより、研究した制御因子間で交互作用がないと仮定したことが正しいと予測して良いと判断した。したがって、図４に示した設計情報が実物に通用すると考えられる。
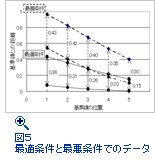
　 参考に、最適条件と最悪条件の生データ図を図５に示す。




前へ <1.2.3.4.5.6.7.8.9.10.11.12.13.14.15.16.17.18.19> 次へ