建設系エンジニアのための地下構造物三次元FEM事始め伊藤忠テクノソリューションズ(株) 野口 利雄
第1講 ボックス地中構造物の3次元設計アプローチ
荷重と構造物要素について(Step2)
はじめに
二次元解析での荷重は、以下の2種類が一般的です。
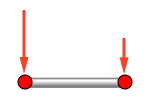
(1)節点集中荷重 |
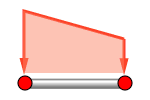
(2)要素分布(一様分布/線形分布)荷重 |
 |
 |
一方、三次元解析でシェルモデルに対する荷重では、面外圧力荷重も加わります。考えられる荷重は以下の3つです。
(1)節点集中荷重 |
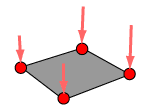
(2)圧力荷重 |
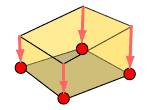
(3)シェル要素荷重 |
 |
 |
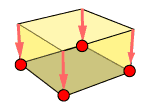 |
ここで、(4)の「圧力荷重」は入力は簡単なのですが、要素上の一様垂直圧力荷重であり、要素構成節点の全てで同荷重値となるため、厳密には正確ではありません。
今回は、三次元シェル要素モデルと二次元梁要素をモデルの両モデルに、これらの荷重を載荷し比べてみます。そして三次元シェル構造への荷重にはどの荷重が最適か調べてみます。また、要素分割の影響も興味がある項目ですので、その点も考察します。
モデリング及び条件設定
解析対象は図1のような地中構造物で、設計条件を表1のように設定しました。
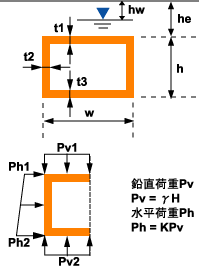 図1 解析対象構造物の形状、荷重 図1 解析対象構造物の形状、荷重 |
|
|||||||||||||||||||||||||||||||||||||||||||||||
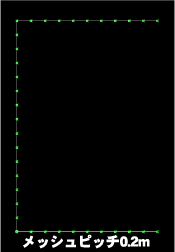
図1の地中構造物を、二次元梁要素と三次元シェル要素でそれぞれ1/2対称でモデル化します。要素分割の粗密の影響を調べるため、二次元、三次元両モデルともメッシュピッチ(要素長)に関して大小2モデルを用意しました。モデル図を図2、図3に示します。
 |
 |
|
| 図2 モデル図(2次元モデル) | ||
 |
 |
|
| 図3 モデル図(3次元モデル) | ||
上記、モデル、荷重を表2に示す組み合わせで合計6ケース解析します。
|
||||||||||||||||||||||||||||||||
解析結果
図4に二次元梁要素モデルを用いた場合(ケース2)の曲げモーメント図を示します。図5に三次元シェル要素モデルを用いた場合(ケース6)の曲げモーメント図を示します。この図は変形も同時に表示しています。
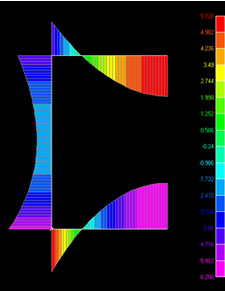 図4 二次元梁要素モデルの曲げモーメント図 図4 二次元梁要素モデルの曲げモーメント図(ケース1) |
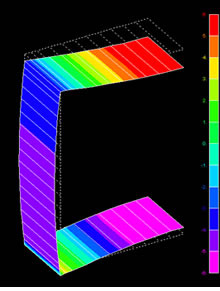 図5 三次元シェル要素モデルの曲げモーメント図 図5 三次元シェル要素モデルの曲げモーメント図(ケース6) |
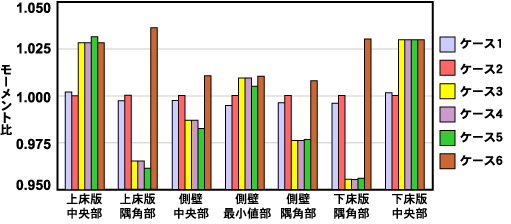
表5に各ケースの解析結果を示します。梁要素モデルの要素細分割モデルケース(ケース2)を基準に各ケースの曲げモーメント比較しました。
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
考察
解析結果より以下の事柄が言えます。
- ケース1とケース2の差は最大0.5%とごく僅かです。要素分割数は梁高さの半分を採用すれば十分と考えられます。
- ケース2(基準ケース)に対するケース3~6の差は最大4.5%です。三次元シェルモデルへの荷重は、やはり実際の荷重を忠実に入力できるシェル要素荷重を用いることが望ましいでしょう。また、梁要素とシェル要素の挙動は等しいとみなせます。
| | Step1 | Step2 | Step3 | Step4 | Step5 | Step6 | |



