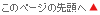マルコフ連鎖モンテカルロ法のアルミリサイクルへの適用

β相安定化に寄与する元素を評価した事例（ハイパーリンク：https://www.engineering-eye.com/THERMOCALC/case02/machine-learning.html#anc_03）に引続き、マルコフ連鎖モンテカルロ法をアルミリサイクルについて適用した事例です。強度・耐食性を有する6000系アルミ合金のリサイクルを例に、合金中の有害相であるβ-AlFeSi相がどの元素がどの程度寄与するかを解析します。また無害化手法として、βをα-AlFeSi（無害相）として晶出させることがあります。ここで紹介する事例として、溶体化処理時に有害相をなるべく生成させない設計ということで、有害相と無害相に対する元素の寄与度を評価し、材料分析・設計の指針を検討します。

6000系アルミ合金の成分としてはSiとFe量に関しては固定し、Cu, Mn, Mg, Znの組成のパターンに対して一点平衡計算を繰り返したデータセットを作成しました。有害相形成の抑制に寄与しうる元素の解析ということで、平衡計算で得られた有害相（β-AlFeSi相）と無害相（α-AlFeSi）の相分率を目的変数としたデータセットを作成しました。
散布図では、SiとFe量は固定し、合金元素の元素量に対する有害相の生成量を示します。Mnについては有害相との関連性/傾向は見られていますが、元素どうしの影響も関係する可能性もあるため、どの元素がどの程度無害相の形成に寄与するかを必ず見られるとは限りません。

各溶質元素に対する有害相分率の散布図

データセットに対して、教師あり学習の回帰モデルを作成します。回帰モデルのランダムフォレスト回帰をインプットとして、MCMCサンプリングを行い、相関をヒストグラムで分析しました。SiとFe量はそれぞれ1wt%の場合で、横軸は各元素の組成で、縦軸が生成する確率密度を示します。赤色のバーは、相の割合が大きくなる時の組成、青色のバーで相の割合が小さくなる時の組成を示します。Cuには明確な傾向は無く、Mnについては添加量が少ないと、有害相の生成する割合が大きくなる確率が増えますが、ある程度入れれば有害相はほとんど生成しないということも示されています。Mgは添加量が少ないと、有害相の生成する割合が大きく、ある程度入れれば生成する割合が小さくなる確率が得られています。Znは添加量が多いと、有害相が生成する割合が大きくなる確率が増えます。

溶質元素に対する（Si:1, Fe:1wt%）有害相の相分率が高く（赤）/ 低く（青）なる
確率を示すヒストグラム

SiとFe量が極端に多い場合（Si:3, Fe:9wt%）ですが、Mnを添加していない場合には有害相が多くなる可能性は高く、若干添加されているだけで有害相が生成する割合が小さくなる確率が高くなります。Si・Feが極端に多い場合でも、Mnを2wt%入れることで有害相はほとんど生成されない可能性があることが示されています。

溶質元素に対する（Si:3, Fe:9wt%）有害相の相分率が高く（赤）/ 低く（青）なる
確率を示すヒストグラム

Mnと同じような無害化に貢献するような元素の探索を行いました。候補としたのはCr,Ti,Niです。Mn, Cr, Ti, Ni以外の元素は固定で、同じようなアプローチで評価しました。
Crについて、若干添加するだけで有害相が生成する確率は一気に小さくなります。一方でTiとNiに関して、今回のケースでは相関は無いという結論になりました。

溶質元素に対する（Si:1, Fe:1wt%）有害相の相分率が高く（赤）/ 低く（青）なる
確率を示すヒストグラム

積層造形用のチタン合金における組成の最適化

積層造形向け生体材料用チタン合金について、コスト、造形性、密度を両立する合金組成を探索した事例です。コストについては、合金に含まれる元素量や、実際の質量当たりのコストなどから定義します。造形性については、Thermo-Calcの平衡計算で得られる固相線温度と液相線温度の差（凝固温度幅）から評価します。密度については、Thermo-Calcの平衡計算で得られる組織情報（相分率、組成）から取得します。
これらの目的変数はすべて小さくなることが望ましいです。そこで、最適化ライブラリOptunaを利用して多目的最適化を実施しました。OptunaのNSGA-IIサンプラーにより多目的最適化を実施した結果、特に探索後期において全ての目的変数が小さいBest Trial周辺で、合金組成の集中的な探索ができていることがわかります。このように最適化手法を用いることでより効率的な材料設計が可能です。

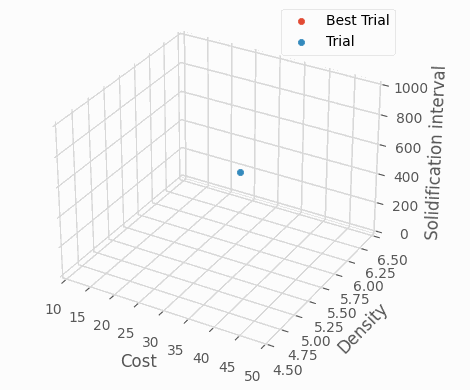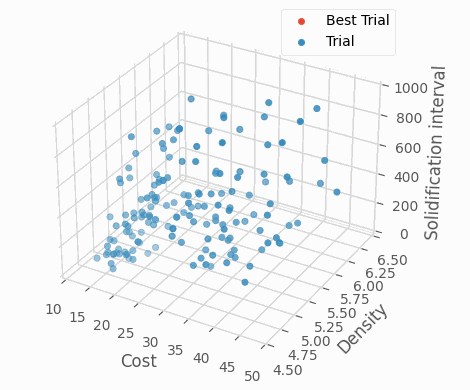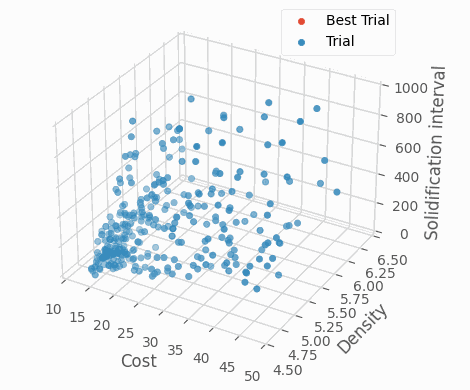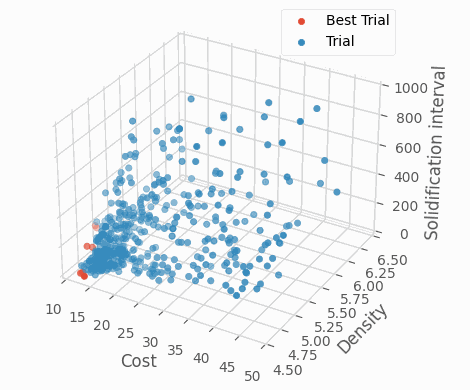
Optunaによる条件探索の様子

ベイズ最適化による凝固割れ感受性のための組成最適化

TC-Pythonとベイズ最適化を用いて、多元系のアルミニウム合金ADC10における耐凝固割れ感受性向上のための組成探索を効率的に行った事例です。

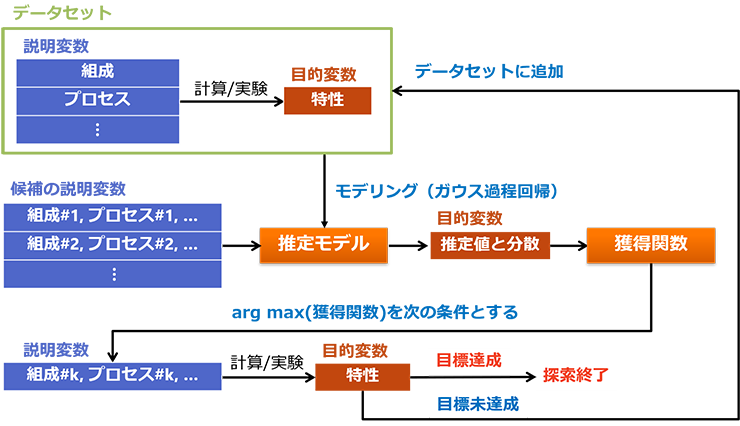
ベイズ最適化の概略図を示します。ベイズ最適化は目的変数を最大化（最小化）するような説明変数を効率的に探索する手法の一つです。既に得られている説明変数と目的変数のデータセットを用いて、ガウス過程回帰によって目的変数の推定モデルを構築します。ガウス過程回帰による推定モデルでは、推定値だけでなくその推定値の信頼性（分散）を得ることができます。そして、各組成の候補から得られた推定値と分散から獲得関数を計算することで次の実験やシミュレーションに使用する条件を決定します。その条件での実験/計算の結果が目標を達成すれば探索を終了し、そうでなければその結果をデータセットに加えて再度この流れを繰り返します。

この事例での目的変数はThermo-Calcで予測が可能な「クラック感受性係数（CSC）」で、説明変数は各元素量です。各元素量についてはADC10の規格の範囲内で探索を実施しました。ベイズ最適化における獲得関数はProbability of Improvement（PI）とExpected Improvement （EI）の2つを使用してそれぞれ組成探索を実施しました。ベイズ最適化との比較のため、ランダムサーチでの探索も実施しました。

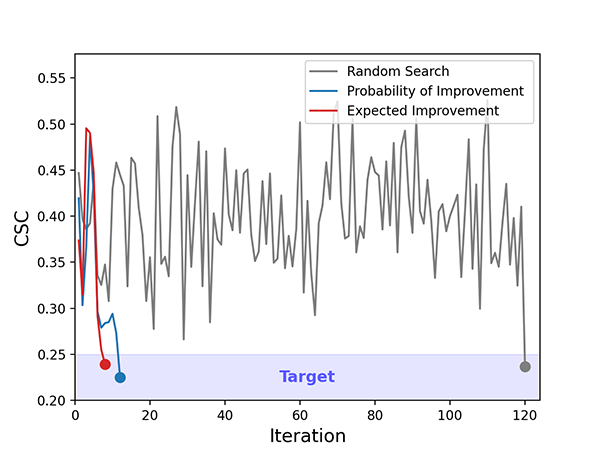
各試行回数におけるクラック感受性係数

CSCが目標値の0.25以下（青い領域）になるまで各手法で組成探索を行った結果をグラフに示します。ランダムサーチでは120回目の試行で目標を達成したのに対し、PIによるベイズ最適化では12回目、EIによるベイズ最適化では8回目の試行で達成し、より効率的な組成探索を行うことができました。このような機械学習を利用した適応的実験計画法により材料開発をさらに加速することができます。

ベイズ最適化による複数の要件を満たすための組成最適化

ベイズ最適化により、鉄鋼材料SKD61について複数の要件を同時に満たすような組成探索を行った事例です。

前述の事例では目的変数が一つでしたが、実際の材料設計では様々な要件を同時に満たす条件（組成やプロセス）を探索する必要があります。ベイズ最適化の獲得関数Probability of Improvement（PI）は既存のサンプルにおける目的変数の最大値より大きくなる確率のため、各目的変数のPIの積を獲得関数とすることで目的変数が複数の場合にも対応することができます。この事例では「焼入れ性」、「焼入れ時の熱コスト」、「焼戻し時の二次硬化」の3つを同時に満たす要件としています。これらはそれぞれ「上部臨界冷却速度」、「A3線温度」、「フェライトからのM2C炭化物の駆動力」に対応するとしてThermo-Calc（TC-Python）で計算しました。ベイズ最適化の有効性を示すため、ランダムサーチでの探索も実施しました。

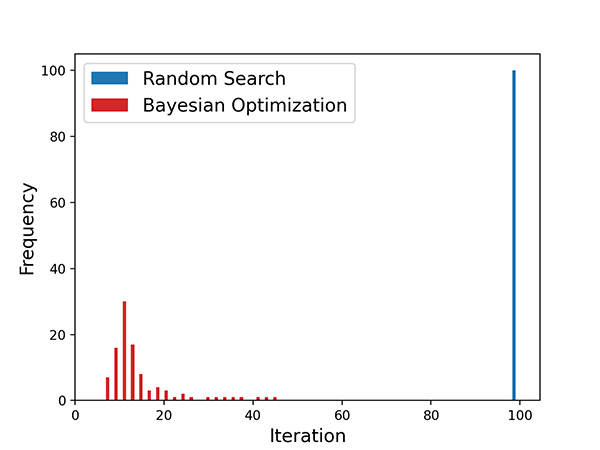
要件を満たす組成探索を終了するために要した試行回数

ベイズ最適化とランダムサーチによる探索において、全ての目的変数で同時に目標値を超えた試行回数のヒストグラムを示します。1回の探索に対し、100回の試行回数を上限としましたが、ランダムサーチでは100回の探索を実施したものの、一度も100回の試行回数で同時に目標値を超える条件を見つけることができませんでした。一方でベイズ最適化では、平均14回の試行回数で探索を終了することができました。

機械学習の解釈手法の適用

マテリアルズ・インフォマティクスにおいて材料特性や新規物質などの予測モデルを構築する際には、予測するだけではなくモデルの解釈性も重要です。モデルの振る舞いを理解することで、事前知識との整合性の確認や新たな知見の発見などに役立てることができます。本事例では、Shapley Additive exPlanations（SHAP）という機械学習モデルがなぜそのような予測値を出力したのかを説明する手法を用いて、Thermo-Calcで生成したデータセットに対して分析しました。

鋳物用アルミニウム合金ADC10を対象に、Thermo-Calcで計算可能な凝固割れ感受性係数を目的変数、各元素量を説明変数としたデータセットを作成しました。凝固割れ感受性係が大きいほど凝固割れが起こりやすいと解釈できます。このデータセットを用いて Light Gradient Boosting Machine（LightGBM）にて予測モデルを構築しました。このモデルとテストデータを用いてSHAP値を計算しました。

テストデータ中の1つのインスタンスについて、SHAP値を可視化した図を示します。

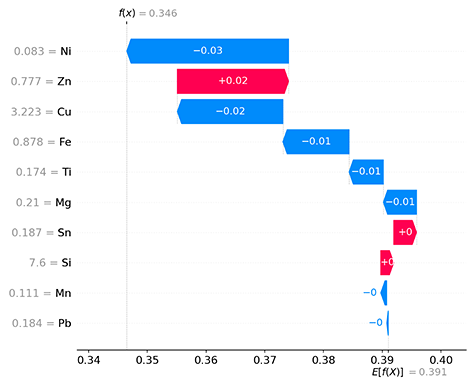
Al-0.083Ni-0.777Zn-3.223Cu-0.878Fe-0.174Ti-0.21Mg-0.187Sn-7.6Si-0.111Mn-0.184Pb（wt%）における各特徴量の貢献度

予測値の平均E [f (X) ] が0.391に対して、このインスタンスの予測値f (x) は0.346と平均よりも低い値が予測されています。貢献度の小さい特徴量から順に足し上げて予測値f (x) が0.346となっており、最も貢献度が大きいのはNi組成による-0.03であることがわかります。このように一つ一つのインスタンスの予測値に対して、そのような値になった理由を知ることができます。

さらに全インスタンスのSHAP値の絶対値の平均をとることで、各特徴量の平均的な重要度を評価することができます。各特徴量の重要度の平均を可視化した図を示します。図より、Cuが最も重要度が高いということが分かります。このようにSHAPはマクロな解釈手法としても利用できます。

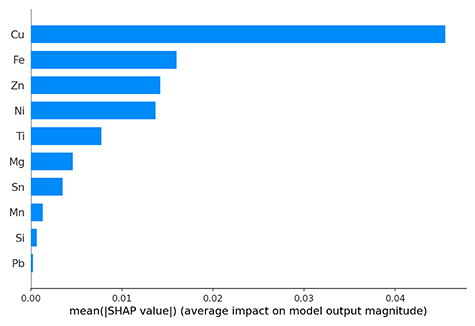
各特徴量の平均的な重要度

各インスタンスの特徴量の貢献度の分布を可視化することもできます。点が赤いほど特徴量の値が大きく、点が青いほど特徴量の値が小さいことを意味します。この図から、特にCuの組成が大きいほど凝固割れ感受性係数の低下（凝固割れ性改善）への寄与が大きいことがわかります。

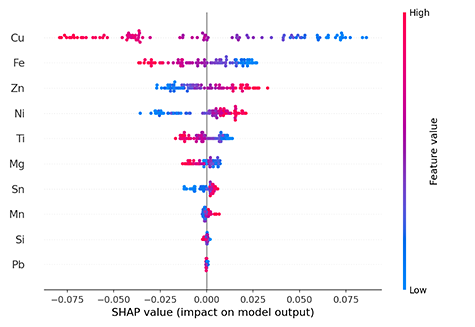
各特徴量の貢献度の分布

機械学習モデルとマルコフ連鎖モンテカルロ法による相関関係の可視化

β型チタン合金について、「平衡状態におけるβ相の量」と3つの「溶質元素」の相関関係を可視化した事例です。どの条件が材料特性にどのような影響を及ぼすかを理解することで、材料設計の指針を立てることができます。しかしながら実用合金での設計パラメータは多変数であり、それぞれの変数についての影響を理解することは容易ではありません。先行研究で提案されている、機械学習モデルとマルコフ連鎖モンテカルロ法（Markov Chain Monte Carlo methods; MCMC）により非線形な相関関係を可視化する手法[1]を用いて、材料解析を実施しました。

β型チタン合金として、TiにNb, Sn, Zrを添加した合金を対象としました。ランダムな50000通りの温度と溶質元素の組成のパターンに対し、Thermo-Calcで平衡計算を行いました。なお50000通りの計算は手作業で実施することは現実的ではないため、TC-Pythonライブラリを使用しました。温度と溶質元素の組成を説明変数、平衡計算で得られたβ相の相分率を目的変数とするデータセットを用いて、ランダムフォレスト回帰で予測モデルを構築しました。

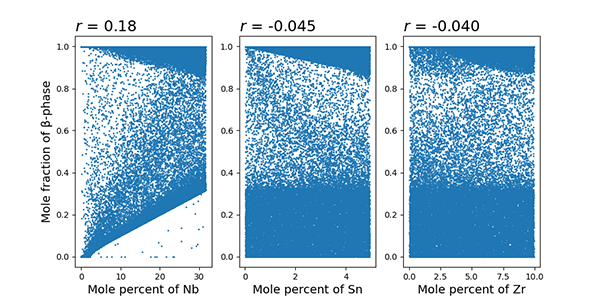
β相の相分率と各溶質元素における散布図とピアソンの相関係数

「平衡状態におけるβ相の相分率」と「各溶質元素の組成」の散布図とピアソンの相関係数rをグラフに示します。いずれの相関係数も0に近く、線形な相関関係を有していません。

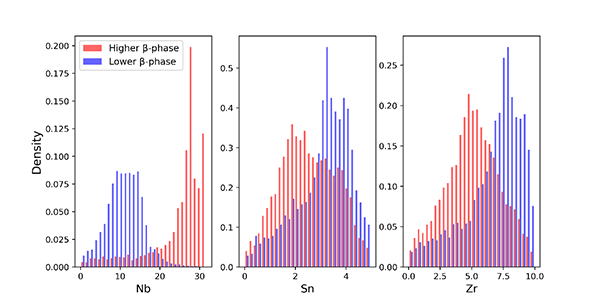
β相の相分率が高く（赤）/ 低く（青）なるための溶質元素の組成のヒストグラム

回帰モデルとMCMCによりサンプリングされた各溶質元素の組成のヒストグラムを示します。β相が多くなるためにはNbの添加量を増やす、もしくはSn, Zrの添加量を減らす必要があることが示されています。Nb, Snはそれぞれβ相安定化、α相安定化の指標であるMo当量、Al当量[2]と対応しており、一般的に知られている傾向と一致します。また、ZrはNbの存在下ではβ相安定化元素として作用することが報告されていますが[3]、本合金系ではβ相安定化のために添加量を減らす必要があることがわかりました。これは平衡計算において、ZrやSnの添加量増加に伴い金属間化合物Zr5Snが生成すると予測されるためであると考えられます。本手法を用いることで、単純な相関分析では抽出が困難な非線形な相関関係を捉えることができました。

[1] Tamura, Ryo, et al. "Materials informatics approach to understand aluminum alloys." Science and technology of advanced materials 21.1 (2020): 540-551.
[2] 小柳禎彦. "耐熱チタン合金の開発史について." まてりあ 58.4 (2019): 188-192.
[3] Long, Marc, and H. J. Rack. "Titanium alloys in total joint replacement—a materials science perspective." Biomaterials 19.18 (1998): 1621-1639.

ニューラルネットワークによるマルチフェーズフィールド法の高速化

熱力学データベース連携のマルチフェーズフィールド法にニューラルネットワークを適用し、高速な凝固シミュレーションを実現した事例です。

ニューラルネットワークは任意の関数を近似できることが一般的に知られています。また、小規模なニューラルネットワークであれば入力から出力の計算が非常に速いというメリットがあります。

マルチフェーズフィールド法はミクロ組織を予測するための手法として広く使われている手法です。特にCALPHADに基づく熱力学データベースと組み合わせることで実用合金である多元系合金の凝固計算を行うことができ、材料の特性を知るのに非常に有効な手法の1つとなっています。一方で、熱力学データベース連携でのマルチフェーズフィールド法は計算のステップごとに計算領域の各点において熱力学計算をして温度・組成からギブスエネルギー・化学ポテンシャルを求める必要があり、それが計算時間のボトルネックになるという問題がありました。そこで熱力学計算をニューラルネットワークに置き換えることで計算の高速化を図りました。ここで、ニューラルネットワークを学習させるためには教師データ、すなわち温度・組成-ギブスエネルギー・化学ポテンシャルの関係を大量に作成する必要があります。今回はThermo-Calc のプログラミングインターフェースであるTQ-Interfaceによって教師データの作成をしました。

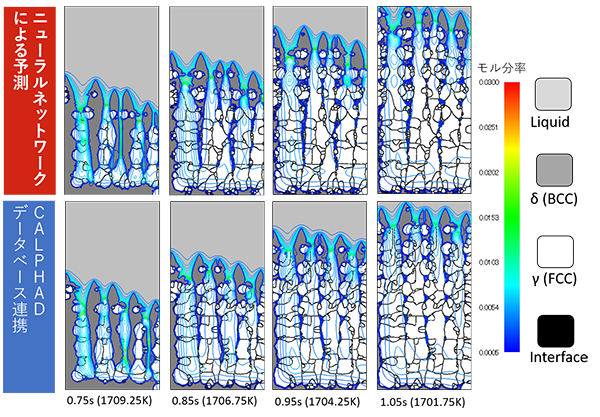
計算結果として上図にマルチフェーズフィールド法計算におけるギブスエネルギー・化学ポテンシャルの算出にニューラルネットワークの予測を用いた場合と、従来の手法であるCALPHADデータベースによる熱力学計算を用いた場合の計算結果の比較を示します。このようにニューラルネットワークに置き換えて従来の手法の計算結果とほぼ変わらないことが確認できます。また計算速度の向上として従来の熱力計算と比べた場合おおよそ5倍ほどの高速化が実現することも確認しました。