コラム:衝撃・安全
科学エンジニアリング第1部 技術第2課 阿部 淳
[2023/03/30]
前回の「いろいろな弾性波(その1)」で積み残した「③棒の縦振動の速さ」について数値シミュレーションを通して出来るだけわかりやすく考えてみようと思います。おさらいとして、いろいろな弾性波速度の定義式と鉄鋼での値を表1に示します。鋼材の物性値は前回の「いろいろな弾性波(その1)」と同じ値を使用します。
表1 いろいろな弾性波速度の定義式と鉄鋼での値
| 項目 | 定義式 | 鉄鋼での速度 |
|---|---|---|
| ①自由固体の縦波の速さ | 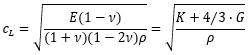 |
5929 m/s |
| ②自由固体の横波の速さ | 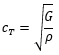 |
3169 m/s |
| ③棒の縦振動の速さ | 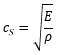 |
5110 m/s |
| ④バルク弾性波の速さ (気体・固体中の音速) |
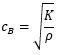 |
4665 m/s (液体と仮定) |
今回の解析モデルは図1のようになります。非常に長い丸鋼材を2本用意し、静止した丸鋼の端部にもう一方の丸鋼をまっすぐに衝突させて、2か所の計測位置で圧力波形を出力しましょう。現実にやろうとするとまっすぐ衝突させるのは至難の業なのですが、ここでは2本の丸鋼がずれたり折れ曲がったりせずに、常に同一軸上で動くものと仮定します。解析は2次元軸対称体系で実施しました。
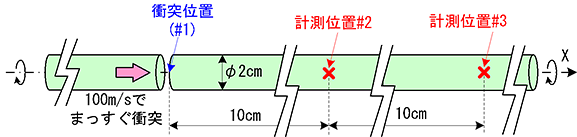
図1 丸鋼同士の衝突解析モデル
解析で得られた圧力コンターの動画を図2に示します。図中の番号1が衝突位置、番号2および3が圧力計測位置です。衝突した位置から複雑な圧力波が2本の丸鋼内に伝播することが分かります。
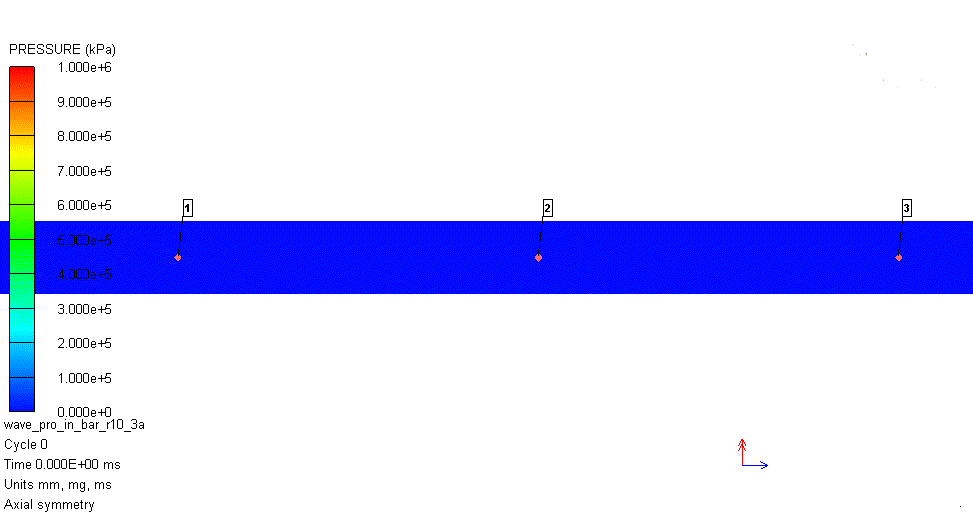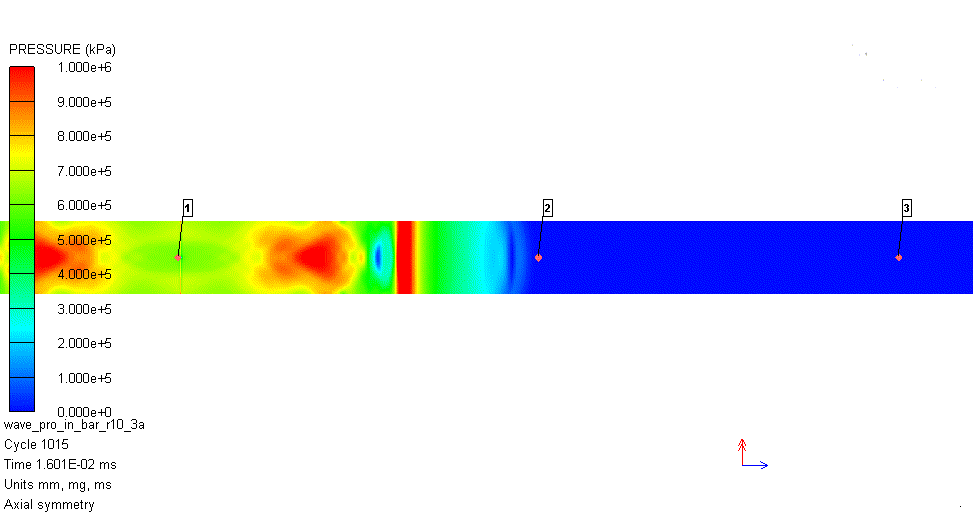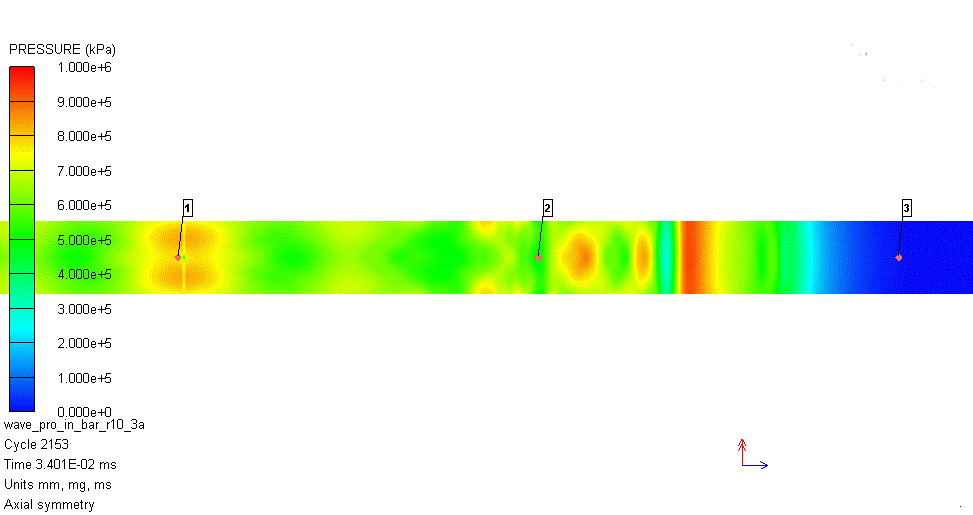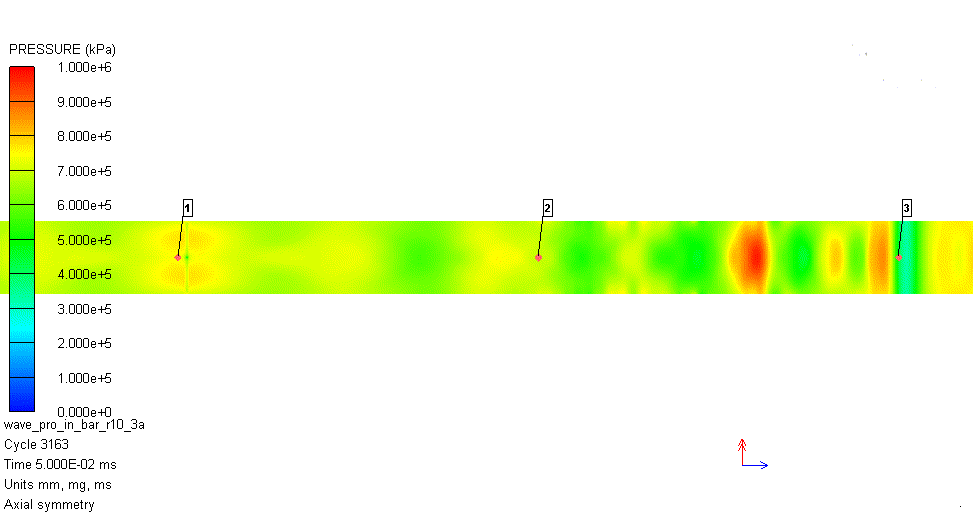
図2 解析結果(径方向拘束なし)
さて、ここでもう1つ条件を加えた解析を行ってみましょう。丸鋼が半径方向に膨らんだり縮んだりしないように半径方向の変位のみを拘束します。ただし、拘束するのは半径方向のみで、丸鋼の軸方向(衝突方向)の変位は拘束しないようにします。解析で得られた圧力コンターの動画を図3に示します。今度は衝突した位置(#1)から単純かつ一定の圧力波が伝播します。

図3 解析結果(径方向拘束あり)
この2つの解析それぞれにおいて圧力計測位置#2と#3で得られた圧力時刻歴を図4に示します。
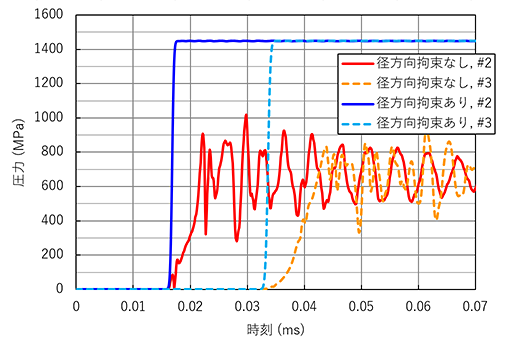
図4 丸鋼内の計測位置における圧力時刻歴
圧力時刻歴においても径方向拘束の影響がきれいに現れますね。この2点間の圧力波の伝播時間から波の伝播速度を計算すると、径方向拘束なしの場合は約5100m/s(圧力波の立ち上がりからピーク値までのどこで計算するか任意性がありますが、ここではおおよその平均的な速度を算出しています)、径方向拘束ありの場合は6010m/sとなります。表1の値と照らし合わせると、前者は「③棒の縦振動の速さ」、後者は(少し速いですが)「①自由固体の縦波の速さ」に当てはまることが分かります。
径方向の変形を拘束すると、衝突時の圧縮状態は径方向には伝わらず、軸方向(衝突方向)のみにしか伝わりません。しかも、衝突する丸鋼は十分に長く、一定速度で押され続けることから、圧力波は一定になると考えることができます。また、径方向拘束は「対称面」と同様の働きをしますので、いわば「径方向に同じように動く物体が無限に存在する」ということになります。
一方、径方向の変形を拘束しない場合、衝突時の圧縮状態は丸鋼がすぐに径方向に膨らむことで緩和されます。したがって、基本的に圧力波の値は径方向拘束ありの場合よりも小さくなります。なお、膨張した後は収縮、収縮の後は膨張、と径方向に膨張・収縮を繰り返しながら、圧力波は軸方向に伝播します。これが弾性振動となって圧力波形に現れていると考えることができます。今回は100m/sと比較的高速度で衝突させたため顕著な弾性振動が生じましたが、衝突速度を小さくしていくとこの振動も小さくなり、どこかでほぼフラットになると考えられます。
最後にまとめますと、「棒の縦振動」は「縦波」に径方向の膨張の影響が重なったもの、ということが今回の2つの数値シミュレーションで明らかになったのではないかと思います。