コラム:衝撃・安全
科学エンジニアリング第1部 技術第2課 阿部 淳
[2022/11/30]
理科年表には「音(種々の物質中における音速)」というページがあり、様々な気体、液体、固体の音速が掲載されています。気体や液体の音速は1種類ですが、固体の音速については、①自由固体の縦波の速さ、②自由固体の横波の速さ、③棒の縦振動の速さ、の3種類の値が掲載されています。なぜ固体の場合は3種類もあるのでしょうか?気体・液体と固体の音速の違いは?これらの違いについて数値シミュレーションで出来るだけわかりやすく説明してみようと思います。
図1のようにある程度大きさを持つ鉄鋼の塊の面をハンマーでたたくと、内部にどのような波が伝播するでしょうか?まずこの現象を数値シミュレーションで解析して、いろいろな弾性波の伝播の様子を確認してみましょう。解析体系は2次元軸対称体系、鉄鋼の物性は表1に示す通り一般的な値とします。
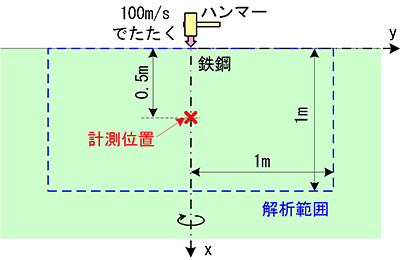
図1 いろいろな弾性波を発生させるための解析モデル概要図
表1 鉄鋼の物性値
| 項目 | 単位 | 値 |
|---|---|---|
| 密度(ρ) | kg/m3 | 7850 |
| ヤング率(E) | GPa | 205 |
| ポアソン比(ν) | ― | 0.2 |
| 体積弾性率(K) | GPa | 171 |
| 横弾性率(G) | GPa | 78.8 |
さて、体積弾性率K、横弾性率G(μと表記する場合もありますがここではGとします)は等方弾性体であればヤング率、ポアソン比から算出できます。
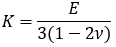
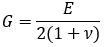
一方、①自由固体の縦波の速さ、②自由固体の横波の速さ、③棒の縦振動の速さ、の定義式と表1の物性値を持つ鉄鋼での値を表2にまとめます。なお、この3つに加えて④として「バルク弾性波」というものを加えます。この呼び方はあまり一般的ではないのですが、定義としては気体・固体中の音速を表したものです。鉄鋼でのバルク弾性波の値は「もしこの世に常温常圧下で液体の鉄鋼が存在したら」という空想上の値と考えてください。
表2 いろいろな弾性波速度の定義式と鉄鋼での値
| 項目 | 定義式 | 鉄鋼での速度 |
|---|---|---|
| ①自由固体の縦波の速さ | 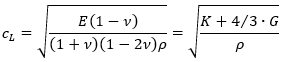 |
5929 m/s |
| ②自由固体の横波の速さ | 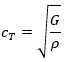 |
3169 m/s |
| ③棒の縦振動の速さ | 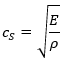 |
5110 m/s |
| ④バルク弾性波の速さ (気体・固体中の音速) |
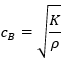 |
4665 m/s (液体と仮定) |
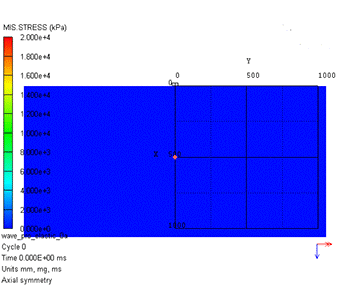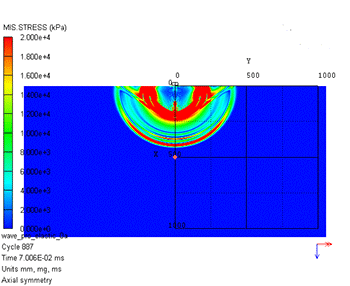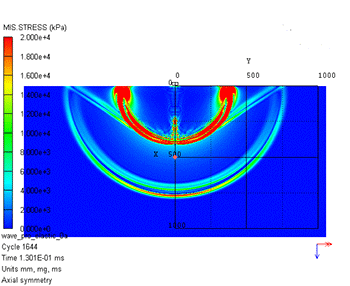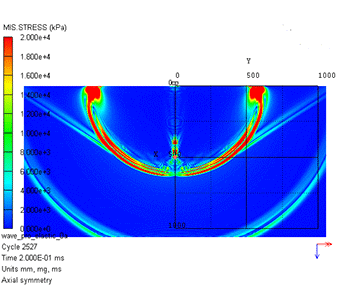
数値シミュレーション結果を図2に示します。左が圧力、右がミーゼス応力のコンター図です。圧力では打撃位置から1つの波動しか確認できませんが、ミーゼス応力では第1波と第2波が確認できます。図3に示すように、この第1波が縦波(P波)、第2波が横波(S波)と呼ばれるものです。表面には打撃位置から表面波(レイリー波)が生じていることもわかります。
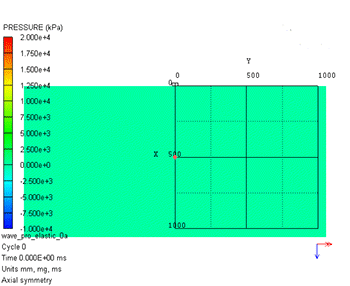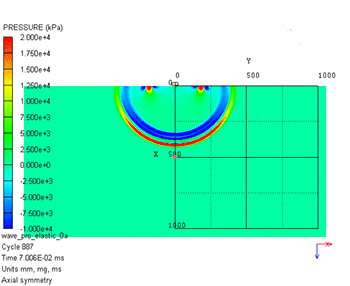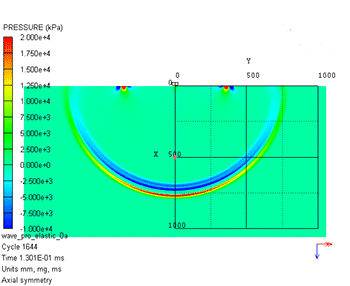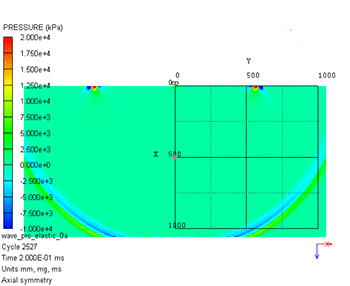
圧力
ミーゼス応力
図2 弾性波伝播の数値シミュレーション結果
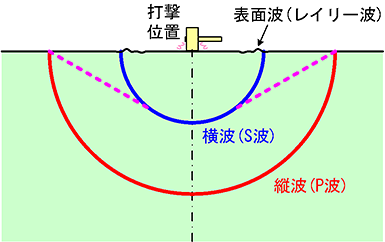
図3 打撃位置からの弾性波の種類
第1波は圧力およびミーゼス応力の両方のコンター図で確認できます。圧力は体積変化(応力の静水圧成分)によって生じます。一方、ミーゼス応力は体積変化(静水圧成分)とは無関係であり、形状変化(応力の偏差応力成分)が支配的となります。したがって、今回現れた弾性波を大雑把に説明すると、第1波は体積変化+形状変化、第2波は形状変化のみ(体積変化は非常に小さい)、となります。
計測位置での各波の到達時刻から弾性波速度を計算してみましょう。図4に打撃位置から鉛直方向0.5mの地点で計測した各弾性波の時刻歴を示します。第1波の到達時刻は0.0853msであり伝播速度は5862m/s、第2波の到達時刻は0.0162msであり伝播速度は3086m/sとなりました。表2の①および②とほぼ同程度の速度になることから、第1波は①の縦波、第2波は②の横波であることが確認できました。青線についてはまた後で説明します。
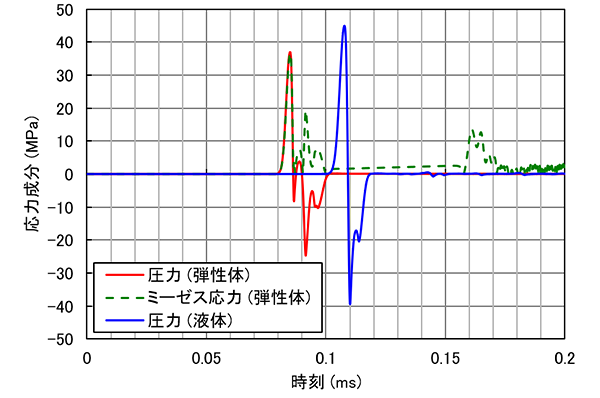
図4 打撃位置から0.5mの地点で計測した各弾性波の時刻歴(その1)
さて、ここで縦波および横波はどのような波なのか具体的に考えてみましょう。先ほどの計測位置における応力の各成分の時刻歴を図5に示します。
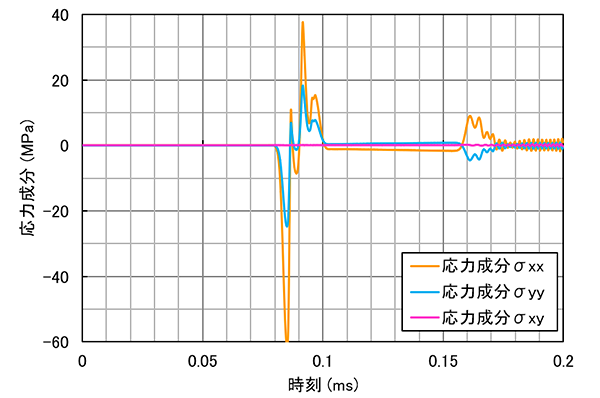
図5 打撃位置から0.5mの地点で計測した各弾性波の応力成分の時刻歴
ここでx方向はハンマーの打撃方向と同一、y方向はハンマーの打撃方向と垂直方向、となります(図1参照)。なお、二次元的に考えると、σxxはx軸に垂直な面に作用するx方向の垂直応力、
σyyはy軸に垂直な面に作用するy方向の垂直応力、σxyはx軸に垂直な面に作用するy方向のせん断応力、を表します(図6参照)。ここでσxy = σyxとなります。
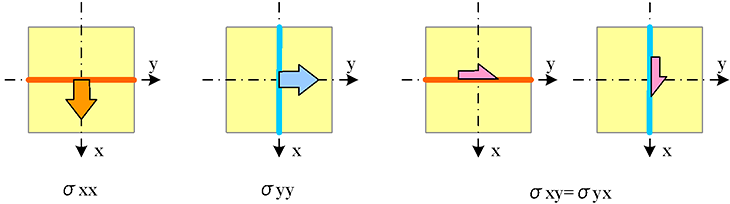
図6 応力成分の作用方向
図5の時刻歴をさらに静水圧成分と偏差応力成分に分けてみましょう。二次元での応力状態は先ほどのσxx、σyy、σxy (=σyx) を使用して以下のように表せます。
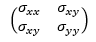
静水圧成分は垂直応力の平均応力σmを用いて表せます。三次元ではσm = (σxx + σyy + σzz)/3 となります。なお、平均応力σmと圧力pは同じ大きさを持ちますが、符号が反対になります(σm = -p です。応力は「引張が正、圧縮が負」ですが、圧力は「膨張が負、圧縮が正」となるため)。偏差応力成分は上記の応力成分から静水圧成分を除いたものになります。二次元では以下のようになります。
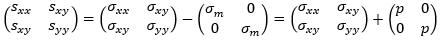
ここで、静水圧成分として圧力p、偏差応力成分としてsxx、syy、sxyの時刻歴を図7に示します。
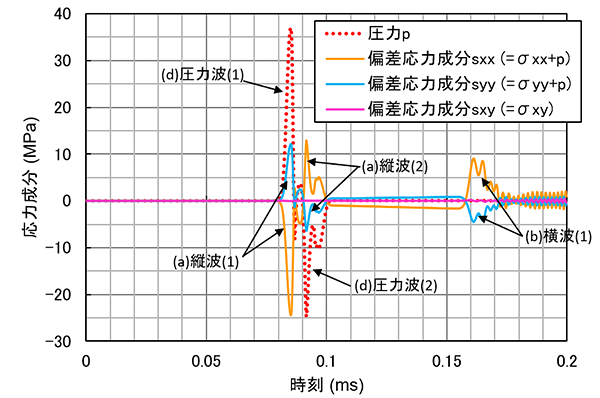
図7 打撃位置から0.5mの地点で計測した各弾性波の応力成分の時刻歴(その2)
すると、垂直応力となるsxx、syyは正負が逆の波形となり、せん断応力はsxyはほぼゼロとなりました。各弾性波の応力成分の変化と形状の変化をまとめたものを図8に示します。圧力と応力それぞれの正負と変形方向の違いにご注意ください。図7と図8から得られた知見をまとめると以下のようになります。
なお、図8に示す形状の変形はあくまで打撃位置直下の計測位置で得られたものであることにご注意ください。また、今回はハンマー速度を100m/sと比較的高速にしたため、第一波は縦波+等方圧縮波(圧力波)となりましたが、ハンマー速度をもっと遅くすると圧力波を伴わない形状変化のみの純粋な縦波が生じるのではないかと思われます。
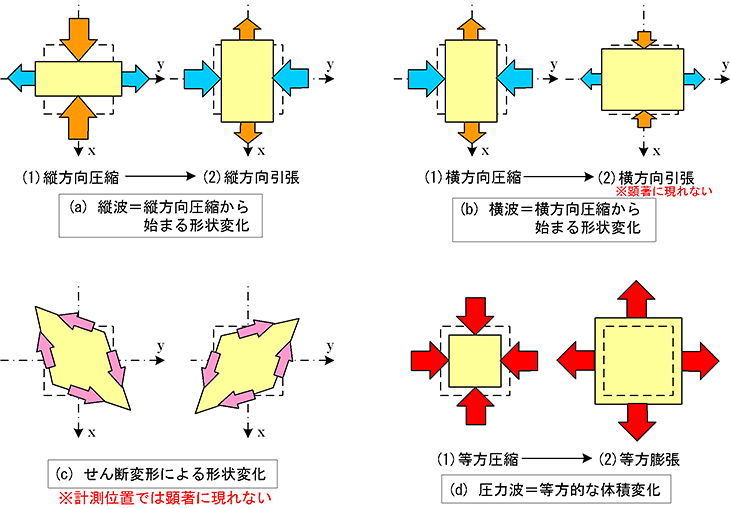
図8 応力成分の変化と形状の変化の関係
最後に「④バルク弾性波」を発生させましょう。バルク弾性波は気体や流体のみに生じますので、先ほどの解析ではバルク弾性波に相当する波が確認できませんでした。そこでここでは「常温常圧下で液体状態の鉄鋼」という空想上の材料を考えます。液体ですので静水圧成分のみしか持ちえません。すなわち、図8のうち (a) (b) (c) の変形は存在せず、(d) の等方的な体積変化のみが可能です。物性値としては表1のうち密度と体積弾性率のみを使用することになります。
図9に鉄鋼を流体と仮定した場合の弾性波伝播の数値シミュレーション結果として圧力コンター図を示します。圧力コンター図からは半球状に広がる1つの波動のみが確認できます。なお、流体は偏差応力成分を持たないことからミーゼス応力は常にゼロとなり、ここでは役に立ちません。
打撃位置から0.5mの地点で計測したバルク弾性波の時刻歴は図4の青線で示したものです。バルク弾性波の到達時刻は0.108msであり伝播速度は4630m/sとなりました。表2の③とほぼ同程度の速度になることから、これがバルク弾性波であることが確認できました。

図9 鉄鋼を流体と仮定した場合の弾性波伝播の数値シミュレーション結果(圧力コンター図)
今回は「③棒の縦振動の速さ」については説明できませんでした。これは細い棒の解析モデルを使用した数値シミュレーションが必要です。また次の機会に説明できればと思っています。