事例紹介
Neural Network MD
SWCNTの格子熱伝導率
カーボンナノチューブの熱伝導率を理論的に評価する手法として、これまで古典分子動力学法が主に用いられてきました。しかし、従来の古典力場ではカーボンナノチューブの高い熱伝導率を十分に評価することができていません。一方で、第一原理計算を用いた高精度計算では小規模なモデルしか取り扱えないため、カーボンナノチューブの多岐にわたる構造を計算しようとすると計算コストがかかってしまいます。そこで、第一原理計算よりも高速で既存の分子動力学計算よりも高精度なニューラルネットワークMD(NNMD)を用いて単層カーボンナノチューブ(SWCNT)の格子熱伝導率を評価し、第一原理計算および従来の古典力場の結果との比較を行いました。
1.計算モデル
計算に用いたSWCNTのモデルは、カイラリティを(4,4)とし、フォノン計算のためにユニットセルを1×1×3に拡張したスーパーセルを用いました(図1参照)。またユニットセルの内部構造は使用した計算手法で構造最適化しました。
図1. SWCNTの計算モデル
2.計算条件
今回、フォノン特性の計算には実空間変位法を用い、格子熱伝導率は非調和格子動力学より評価しました。計算条件の詳細を表1に示します。
表1. 計算条件詳細
| 計算条件 | 説明 |
|---|---|
| 格子熱伝導率計算 |
|
| 力の計算 |
|
3.計算結果
フォノン分散
図2に各計算方法より得られたフォノン分散曲線を示します。従来の古典力場であるTersoffでは負の振動数が現れてしまい、第一原理計算の結果から大きくずれた結果となりました。一方で、NNMDのフォノン分散の計算結果は、第一原理計算の結果と近いことが分かります。
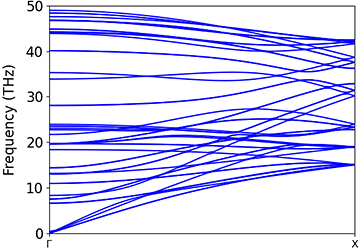
(a)Quantum Espresso結果

(b)NNMD結果

(c)Tersoff結果
図2. SWCNTのフォノン分散曲線の計算結果
格子熱伝導率
図3に各計算方法より得られた格子熱伝導率を示します。従来の古典力場であるTersoffは第一原理計算結果よりも1桁小さな値となりましたが、NNMDの格子熱伝導率は、第一原理計算の結果と近い結果となりました。
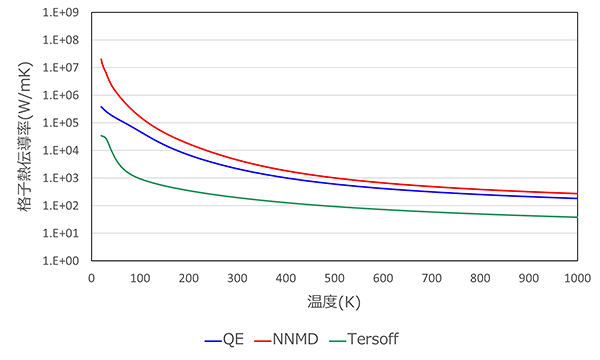
図3. SWCNTの格子熱伝導率の計算結果
以上より、NNMDのフォノン熱特性の計算結果は第一原理計算結果に近く、従来の古典力場と比べて精度が高いことが確認できました。
4.計算コスト
本計算にかかった計算コストを表2に示します。NNMDは第一原理計算と比べて10倍ほど高速に計算できていることが分かります。
表2. 計算コスト
| 計算方法 | 計算コスト(36コア使用時) |
|---|---|
| 第一原理計算 | 60m |
| NNMD | 3m |
| Tersoff | 0.3m |
5.参考文献
[1] T. Tadano, Y. Gohda, and S. Tsuneyuki, J. Phys.: Condens. Matter 26, 225402 (2014)




