コラム:AI・OR・最適化
科学ビジネス企画推進部 プロダクトサービス第2課 綛 宜史
[2023/09/28]
「コンピュータ科学の父」と呼ばれるアラン・チューリングが第二次世界大戦中にドイツ軍の暗号”エニグマ”を解読し連合軍の勝利に貢献したことは今では有名な話ですが、その解読に現代のデータサイエンスに通じる手法が採用されていたことはご存じでしょうか? チューリングが執筆した論文は機密扱いとされ2012年にようやく公開されたことからも、暗号解読技術としての有効性をうかがい知ることができます。
エニグマの解読は、暗号を復号するための復号機側の設定(パラメータに相当)を特定することで可能となります。複合機の設定は膨大な組み合わせが存在しますが、チューリングはベイズ統計学の考え方を用いて復号機の設定を推定することに成功しました。
現在では、ベイズ統計学はデータサイエンスに組み込まれ、さまざまな原因推定やパラメータ推定に応用されています。
本稿では、未知のパラメータを推定する有力な手法である、シミュレーションとベイズ理論を組み合わせたカーネルABC法をご紹介します。
シミュレータは、対象システムをモデル化し、計画情報や既知のパラメータ値を入力することで、システムの出力値を推定します。
ここでは、パラメータの一部が未知であり、システムの出力値が分かっている場合(システムの実測値がある場合)に、未知のパラメータを逆推定することができるかどうかを考えます。
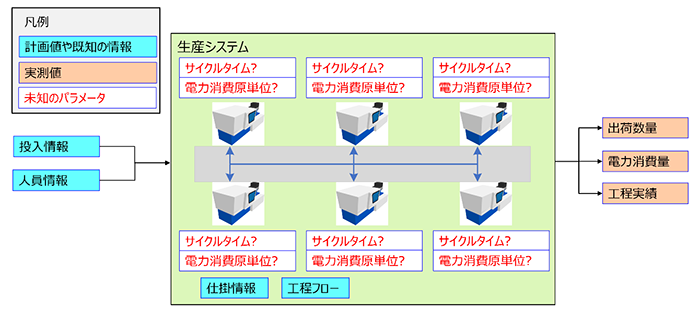
図1. 生産システムにおける未知のパラメータの例
例えば生産システムでは、さまざまなパラメータが存在します。その中で、仕様書に数値が記載されていないものや、仕様書に記載されている数値と実際の数値との間に違いがあるものがあります。そのようなパラメータが推定対象となります。
シンプルなシステムであれば、連立方程式を解くことでパラメータを計算することが可能かもしれませんが、複雑なシステムの場合は数式を表現することが困難になります。また、実測値はノイズが含まれている可能性がありますし、また未知のパラメータもばらつきを持つ確率的なパラメータかもしれません。そのような場合には数値解析的な手法よりも、ベイズ推定による統計解析的な手法を用いる方が有効です。
ベイズ推定とは、ベイズ確率の考え方に基づき、観測事象(観測された事実)から、推定したい事柄(観測事象を引き起こした原因事象)を、確率的な意味で推論することです。
ベイズ推定は、以下のベイズの定理から発展してきた考え方です。
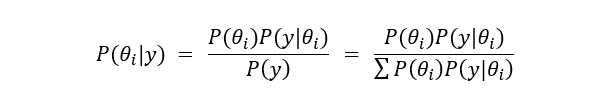
| 記号 | 意味 |
|---|---|
| y | 発生した事象 |
| θi | y が発生した原因の可能性がある事象(原因事象) |
| P(y) | y の発生確率 |
| P(θi) | P(θi) の発生確率(事前確率と呼ばれる) |
| P(y|θi) | θi が原因で y が発生する条件付き確率(尤度関数と同義) |
| P(θi|y) | y が発生したときに、原因が θi だった場合の条件付き確率(事後確率と呼ばれる) |
原因事象 θi が連続値の場合は、以下の式で表現することができます。
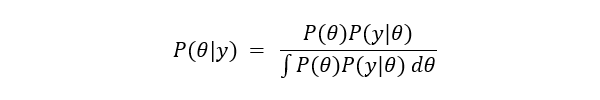
尤度関数が既知であるか、または観測データが豊富にあり条件付き確率分布から尤度関数を求めることができれば、事後確率を求めることができます。事後確率分布が得られれば、以下の式よりパラメータの平均値を求めることができます。
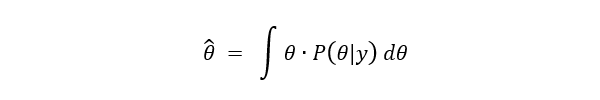
尤度関数が未知の場合あるいは観測データが十分でない場合は、どうすればよいでしょうか? ここで、シミュレーションの出番です。
もし対象をシミュレーションすることができるのであれば、パラメータをランダムサンプリングし、シミュレーションを実行します。シミュレーション結果値が観測値と比較して一定の範囲内εであれば採用、そうでなければ不採用(棄却)とし、シミュレーション計算を繰り返すと、パラメータに対する頻度分布を近似的に作成することができます。
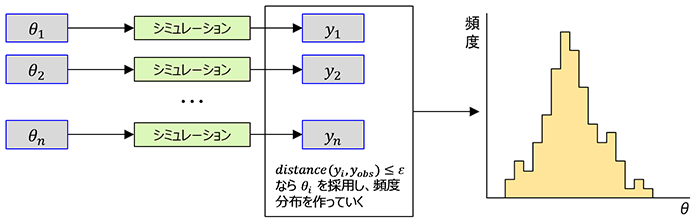
図2. 棄却ABC法
この手法は棄却ABC法(Approximate Bayesian Computation)と呼ばれるものですが、以下のような問題があります。
カーネル法は、データを高次元の特徴空間に写像する方法論で、非線形の対象を線形に扱うことができ、分類や回帰問題に応用されています。また、元の空間が高次元であっても計算量の問題が生じない利点があります。
ABC法にカーネル法を組み合わせて、サンプリング値の加重合計の形でパラメータ推定を可能にしたものが、カーネルABC法です。カーネル法に登場するカーネル関数は、特徴空間におけるデータの内積を計算するものです。特徴空間における内積は言わばデータ同士の”類似度”を表しており、カーネルABC法ではこの類似度からシミュレーションケースごとの重みを計算してパラメータ平均値を求めることができます。
シンプルなABC法では多量のサンプルを捨てていたのに比べ、カーネルABC法ではすべてのサンプルを使用するためサンプリング数を抑えることができます。また、他のABC法に比べて問題に依存した処理が不要であり、観測値が多次元であってもよい性能が得られることが示されています。
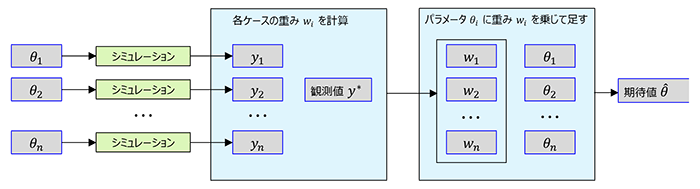
図3. カーネルABC法
2023年3月末に経済産業省・環境省はカーボンフットプリントのガイドラインを公表しており、そこではCFP算定にあたって一次データの活用を推奨しています。
しかし、CFP算定のための一次データ活用にあたっては、幹線単位のエネルギー消費データの把握に留まり製品単位でのGHG排出量算定用途まで詳細に把握できておらず、また、一次データの取得のためのセンサー導入は費用対効果が見通せず進んでいないのが実情ではないでしょうか。
本稿の技術を応用すれば、シミュレータ上に生産ラインを再現してシミュレーションによるサンプリングを行い、カーネルABC法によりCFP算定に必要なパラメータを推定することが可能です。
弊社では、パラメータ推定プログラムを開発し、シミュレーションと組み合わせてCFP算定のための電力消費原単位の推定サービスに適用しております。
本稿で紹介した技術は、生産システムにとどまらずシミュレーションが可能な対象であれば様々なパラメータの推定が可能です。カタログ値で設定しているパラメータを調整してシミュレーション精度を向上することも可能になります。
未知のパラメータの推定やシミュレーション精度の向上に課題がある方は是非ご相談ください。
Intelligent Twinサービス(お問合せフォーム: ページの下部)
https://x-simulation.jp/IntelligentTwin
製造業のGXに向けたデジタルツインソリューションを提供
https://www.ctc-g.co.jp/company/release/20230901-01619.html
生産物流シミュレータ WITNESS
https://www.engineering-eye.com/WITNESS/
S Nakagome, K Fukumizu, S Mano. “Kernel Approximate Bayesian Computation in Population Genetic Inferences”, Statistical applications in genetics and molecular biology, 2013