コラム:衝撃・安全
原子力・エンジニアリング第1部 阿部 淳
[2022/03/31]
鋼鉄やアルミ合金などの金属は人間の腕力程度では自由に形を変えることができませんので「固体」と呼ばれています。しかし、金属でも「流体」のように変形する場合があります。例えば融点を超えるほどの高温になった場合です。溶鉱炉などで真っ赤などろどろの鉄が流れる様子を見たことがあると思います。もう1つの例としては、高速衝突や爆薬によって極めて短時間に超高圧になった場合です(蛇足ですが、時間をかけてゆっくりと超高圧状態になる場合、ほとんどの物質は固体になるようです)。「超高圧」という状態に明確な定義はないのですが、様々な文献を見ますと大体GPa(ギガパスカル)オーダー以上の圧力と考えてよいでしょう。1GPaは1万気圧で、あるとすれば水深10万mでの圧力です。想像もつかない圧力ですね。このコラムではこの「超高圧」おける金属の流体的な挙動についても触れてみたいと思います。
さて、題名に取り上げた「ユゴニオ弾性限界」ですが、理論的な背景や詳細な説明は専門書や技術論文に譲ります。あえて批判を恐れずにWikipediaの説明を引用しますと「固体が塑性変形を開始し流体のように振舞う領域に入る境界線となる圧力」です。この文言だけですと「塑性流動?」とも捉えられなくもないのですが、「極めて短時間に超高圧にする場合」という点において塑性流動とは異なります。しかし、正直よくわからないですよね。私もよくわかりません。そこで、このコラムではアルミ合金の高速衝突現象を数値シミュレーションで解析することで、「ユゴニオ弾性限界」の具体的なイメージをつかんでもらえないかとチャレンジしてみました。なお、以下では「ユゴニオ弾性限界」をHEL(Hugoniot Elastic Limit)と略します。
解析モデルを図1に示します。アルミ合金の円柱(飛翔体)をもう1つのアルミ合金の円柱(標的)に高速衝突させて、標的内の圧力を観察します。衝突速度は50m/s、200m/s、500m/sの3条件です。円柱長さは1mとしますが、円柱の直径は十分に大きいものとします。円柱端部から希薄波が入ってきますと、圧力波形が複雑になり、訳がわからなくなりますので、これを除去するためです。理想的な1次元現象になりますね。圧力出力点は衝突位置から200mmごとに設定しました。
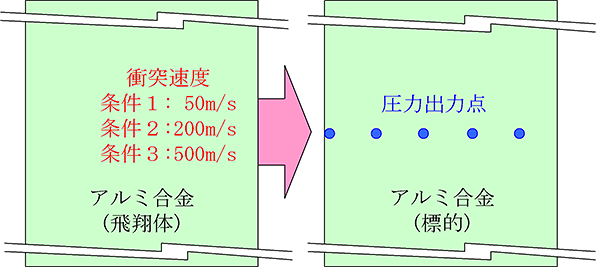
図1 高速衝突の解析モデル概要図
はじめに衝突速度50m/sの場合の各出力点における圧力時刻歴を見てみましょう(図2)。衝突圧は300MPa(=0.3GPa)の高圧状態(ちょっと超高圧には届かなかった)となり、金属内に平面衝撃波が伝播することがわかります。この結果については想像した通りかなと思います。
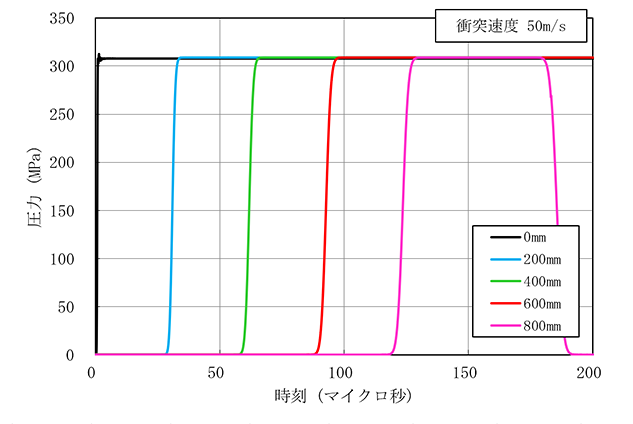
図2 衝突速度50m/sにおけるアルミ合金内の圧力時刻歴
次は衝突速度を200m/sまで上げてみましょう。図3に各出力点における圧力時刻歴を示します。衝突圧は約1400MPa(=1.4GPa)のGPaオーダーの超高圧状態になりました。先ほどと同様に金属内に平面衝撃波が伝播しますが、伝播するにつれて衝撃波の圧力波形の400MPa付近に折れ曲がりが生じます。これは一体どのようなメカニズムで生じるのでしょうか?
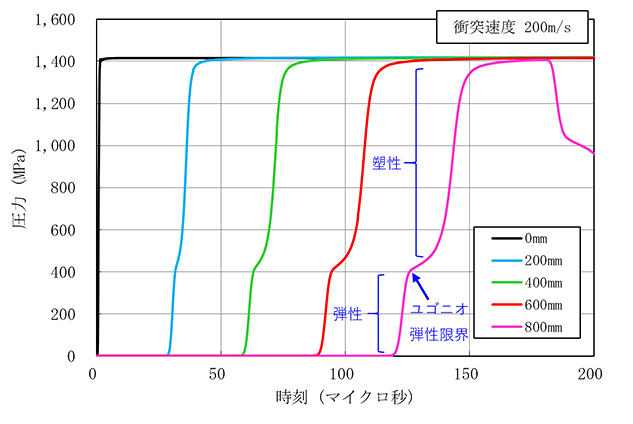
図3 衝突速度200m/sにおけるアルミ合金内の圧力時刻歴
図4に応力-ひずみ関係の模式図を示しますが、この400MPa付近での折れ曲がりは、応力が弾性域から降伏応力に到達して、塑性域に入ったタイミングで発生するようです。応力-ひずみ関係の傾きが変わりますと、波の伝播速度も変化します。傾きが急なほど伝播速度は速くなります。弾性域の波は塑性域の波よりも伝播速度が速いため、衝突位置から遠方になるにつれて伝播速度の違いが顕著となり、このような段差が発生するようです。この段差の開始部分の圧力が「ユゴニオ弾性限界(HEL)」となります。
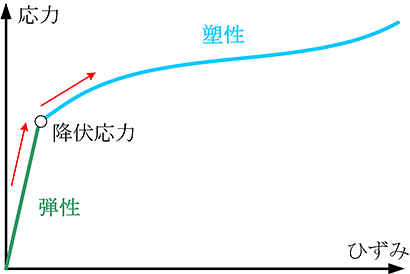
図4 応力-ひずみ関係の模式図
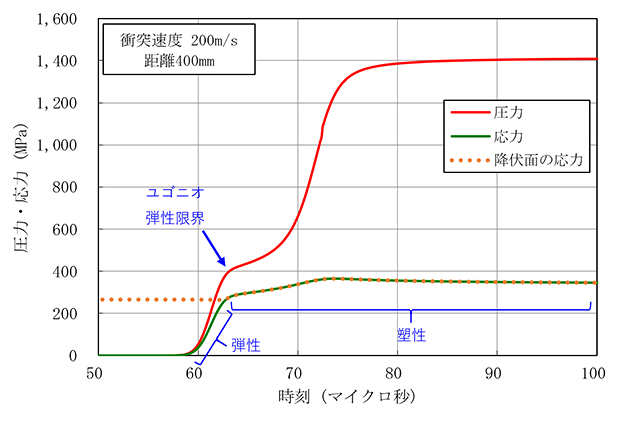
図5 衝突速度200m/sでの距離400mmにおける圧力と応力の時間関係
図5に解析で得られた距離400mmにおける圧力と応力の時間関係を示しました。衝撃波の先頭が到達してから数マイクロ秒で応力が降伏面応力に到達しますが、これとHELのタイミングが一致していますね。その後、応力は降伏面応力と完全に一致しますが、これはこの位置での材料が塑性域に入っていることを示しています。なお、降伏面応力が時間とともに変化するのは、加工硬化(ひずみに応じて降伏面応力が高くなる)、ひずみ速度依存(変形速度に応じて降伏面応力が高くなる)の効果を考慮しているためです。塑性域における応力波形と圧力波形の曲がり具合のタイミングもほぼ一致していますね。
さて、さらに衝突速度を上げるとどうなるのでしょうか?衝突速度を500m/sにした場合の圧力時刻歴を図6に示します。衝突圧は約3800MPa(=3.8GPa)の超高圧状態になりました。金属内を伝播する衝撃波は衝突速度200m/sと同様に二波構造となり、圧力400MPa付近で折れ曲がりが生じます。これがHELとなります。
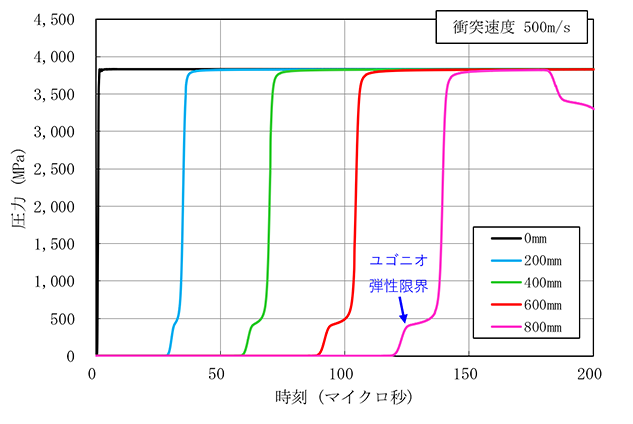
図6 衝突速度500m/sにおけるアルミ合金内の圧力時刻歴
図7に各衝突速度での距離400mmにおける圧力時刻歴を重ねてみました。まず、衝突速度50m/sはHELに到達しない(応力が降伏面応力に到達しない)ため、二波構造とはならないことがわかります。衝突速度200m/sと500m/sではほぼ同時にHELに到達しますが、それ以降の圧力波形は大きく異なっています。さて、図7にはもう1つの条件での結果を加えました。衝突速度は500m/sですが、アルミ合金の材料モデルから構成則を削除して状態方程式のみに変更しました。これは、簡単にいうと、固体特有のせん断変形挙動を無くし、等方圧縮または等方膨張の流体的な変形挙動のみを許すようにしたものです。当然、弾性・塑性(降伏)の区別も無くなります。これと構成則ありの場合と比較すると、圧力上昇はほぼ同一であることがわかります。これはすなわち「HELを十分に超えた超高圧の場合、材料は流体的な挙動を示す」ことを示唆しています。なお、両者に圧力の差が若干生じていますが、これは構成則ありの際に生じる塑性ひずみエネルギーが、構成則なしの場合は等方圧縮のエネルギーに変換された、と考えることで説明できると思います。
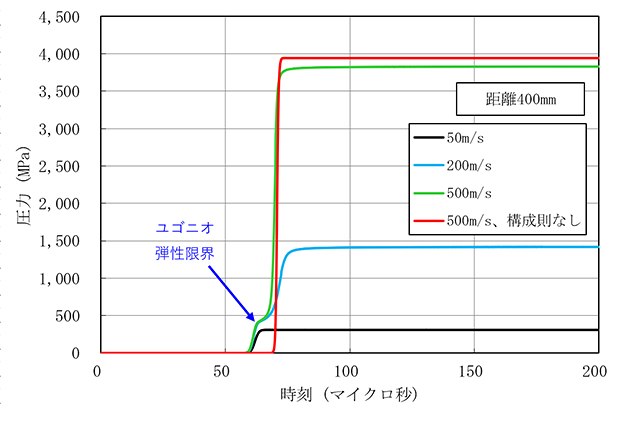
図7 各衝突速度での距離400mmにおける圧力時刻歴の比較
今回のコラムは以上になります。ここまでの説明でHELの具体的なイメージをつかんで頂けたらうれしい限りです。Wikipediaの「固体が塑性変形を開始し流体のように振舞う領域に入る境界線となる圧力」の説明にも納得できたのではないかと思います。今回はアルミ合金に対して解析を行いましたが、このHELは金属だけでなく、セラミックや岩石などにも現れます。
なお、本コラムの主題から外れてしまいますが、材料によっては超高圧において相転移が発生し、HELと同じように衝撃波の圧力波形が折れ曲がる場合があります。そのときは相転移を考慮した材料モデルを使用しないと相転移後の衝撃圧を正しく計算できないので注意する必要があります。
そのほかの高速衝突シミュレーションについてはこちら
https://www.engineering-eye.com/AUTODYN/case/impact/11_longrod.html