Gurobi Optimizerとは

Gurobi Optimizerは、2009年に米国Gurob Optimization社が開発した数理最適化ソルバーです。1988年に発売され現在も広く利用されているCPLEXの生みの親であるRobert Bixbyを含むメンバーが起業し、現代のハードウェハアーキテクチャに合わせて１からソースコードを書き起こして開発したソフトウェアです。
バージョン9の時点で、以下のような幅広い計算領域をサポートしています。

• 線形計画（LP：Linear Programming）
• 混合整数計画（MIP：Mixed Integer Programming）
• 二次計画（QP：Quadratic Programming）
• 二次制約計画（QCP：Quadratic Constraint Programming）
• 二次整数計画（MIQP, MIQCP）
• 二次錐計画（SOCP：Second-Order Cone Programming）
• 非凸二次計画（non-Convex QP, QCP, MIQP, MIQCP）
• 非線形計画の一部（NLP：Non Linear Programming, non-Convex NLP）

非凸二次計画はバージョン9でサポートされるようになり、一般的な多項式で表現できる計画問題を扱うことができるようになりました。

非凸二次計画問題とは

二次計画問題とは、目的関数または制約条件あるいはその両方に二次の変数の項が含まれる問題のことです。非凸とは、制約条件式で囲まれる空間が凸型ではなく、凸凹している空間であることを意味します。
一般に凸型問題は効率の良い（多項式オーダーの時間で計算可能な）アルゴリズムが存在すると言われますが、非凸型問題は一般にNP困難に分類されます。
以下は、非凸二次計画問題の一例です。

目的関数： x → maximize

制約条件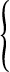： x + y + z ≤ 10
xy ≤ 2
xz + yz = 1

Gurobi Optimizerにおける非凸二次計画問題の計算処理の概要

Gurobiは二次制約式を双線形制約（bilinear constraints）と線形制約に変換します。
例えば前述の以下の式：

xz + yz = 1

は、双線形変換を行い以下の数式に展開できます。

p₁ = xz
p₂ = yz
p₁ p₂ = 1

その後、マコーミック緩和・分枝限定法・切除平面法・動的な制約式の係数の調整を行いながら、グローバルな最適化を実行します。

Pythonによる計算例

以下の問題を計算するpythonのコーディング例をご紹介します。

目的関数： x → maximize

制約条件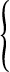： x + y + z ≤ 10
xy ≤ 2
xz + yz = 1

pythonのソースコード：

# 変数の定義
x = m.addVar(name="x")
y = m.addVar(name="y")
z = m.addVar(name="z")

# 目的関数のセット: #maximize x
m.setObjective(1.0*x, GRB.MAXIMIZE)

# 線形制約式の追加: x + y + z <= 10
m.addConstr(x + y + z <= 10, "c0")

# 二次制約の追加 (1) : x * y <= 2
m.addConstr(x*y <= 2, "bilinear0")

# 二次制約の追加 (2) : x * z + y * z == 1
m.addConstr(x*z + y*z == 1, "bilinear1")

# 双線形モデルの計算 (xが実数変数のケース)
m.Params.NonConvex = 2 # 非凸問題を示すパラメータを設定
m.optimize()

m.printAttr('x')

# xを整数変数として定義して再度計算 (xが整数変数のケース)
x.VType = GRB.INTEGER
m.optimize()

m.printAttr('x')

実行結果：

変数	x が実数変数のケース	x が整数変数のケース
x	9.89898	9
y	0	0
z	0.10102	0.111111

まとめ

モデル化の過程で二次式になってしまった場合には、これまではなんとか一次式に落とし込む努力をする必要がありましたが、Gurobi Optimizerが非凸MIQCPを扱えるようになったことでまずはそのまま非凸MIQCPで解いてみるということが可能になりました。モデルを自然な形で表現できることでメンテナンス性の向上やモデル開発期間の短縮につながると期待されます。
Gurobi Optimization社が実施した非凸MIQCPのベンチマークでは、他の非線形ソルバーと比較して計算速度および最適性の面で良好な結果が得られており、実務で活用できる範囲も広がるものと思われます。