コラム:製造・構造
材料・工学技術部 津田 徹
[2020/06/23]
今回は,2019年10月号のCTCサイエンス通信の技術コラム「衝撃問題における応力波の伝播と反射・透過について」(下記URL参照)の続編となります。
http://www.engineering-eye.com/rpt/column/2019/1025_structural.html
前回は,衝撃問題における応力波の伝播に特有な現象である「固定端では同じ大きさの同符号の応力波が反射するのに対し、自由端では同じ大きさの異符号の応力波が反射する」について、1次元弾性波理論を用いて、不連続部における応力波の伝播と反射および透過の観点から説明しました。
今回は、前回のコラムで言及しなかった「固定端での応力は入射応力の2倍になるのに対し、自由端での粒子速度は入射波による粒子速度の2倍になる」についての説明を加え、これらの現象について、固定端と自由端において満足されなければならない境界条件の観点から、数式を極力使わずに図解による判り易い説明を行ってみたいと思います。
応力波が固定端および自由端で反射するときの様子について、ここでは、細い丸棒に大きく重たい剛体が速度Vで衝突し、圧縮の応力が丸棒を伝播する例について考えます。
先ず、図1に示す剛体の衝突により丸棒に生じた圧縮の応力波が固定端に到達してきた状態について考えます。
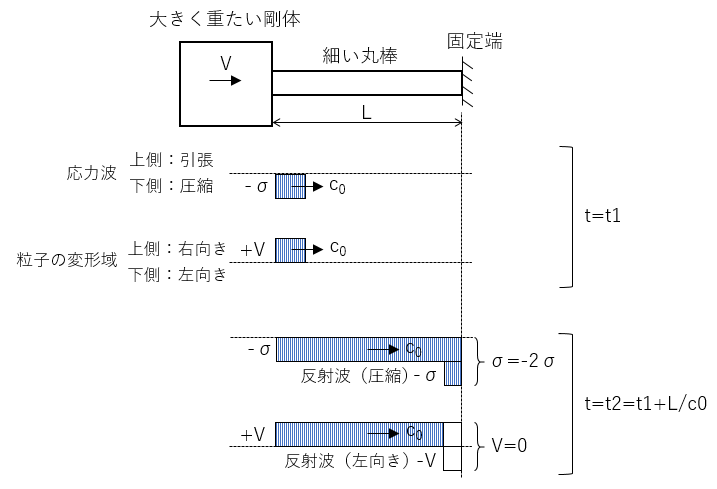
図1 固定端における応力波の反射
大きく重たい剛体が衝突することで圧縮の応力波(大きさ-σで右方向の粒子の変位速度+Vの領域)が細い丸棒を右側に速度c0で伝播していきます(図1の t=t1 の状態)。このとき、応力波が伝播する間も剛体は一定速度で丸棒を押し続けるため、応力波背後の状態は一定となります(実現象としては剛体側にも応力波が伝播して剛体の端部で反射して丸棒側に伝播するため一定にはなりませんが、ここでは“大きく重たい剛体”としていますので、これらの現象は一切無視しています)。
この応力波の先頭が固定端に到達した際、固定端はその名の通り“固定”されていますので、動くことができません。従って、固定端では粒子速度は常にゼロとなります。これは、すなわち、左から入射してきた圧縮の応力波による右方向の粒子速度(+V)と、反射に伴う応力波による左方向の粒子速度(-V)が足し合わされた結果、粒子速度が0になるとも考えることができます(図1の t=t2 の状態)。これはつまり、入射波と反射波の粒子速度の大きさが等しいということであり、衝撃応力の大きさσと粒子速度Vの関係式(σ=-ρc0V )を考えると、応力波の大きさも等しいということになります。このことから、固定端では反射に伴う応力波は入射波と同じ符号を持つ同じ大きさの圧縮の応力波であることが結論付けられることになります。更に、境界では伝播してきた圧縮の応力(σ)と反射した同じ大きさ圧縮の応力(σ)の和となり、固定端での応力の大きさは入射応力の2倍(2σ)となることも判ります。
次に、図2に示す剛体の衝突により丸棒に生じた圧縮の応力波が自由端に到達してきた状態について考えます。
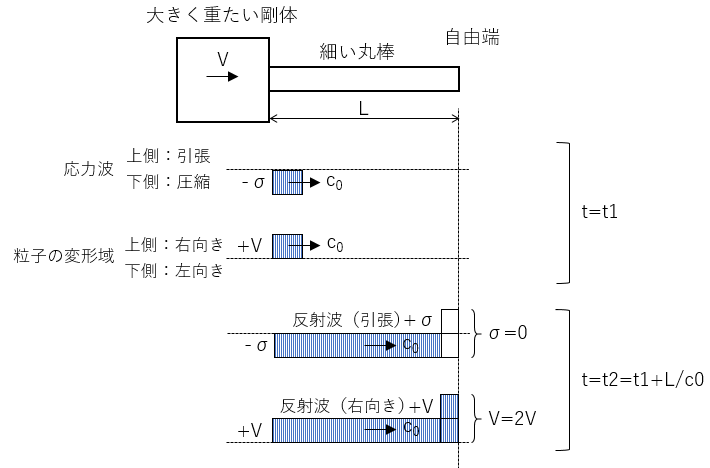
図2 自由端における応力波の反射
応力波の先頭が自由端に到達した際、自由端の外表面はその名の通り“自由表面”であり、そこから先には変形を邪魔(もしくは維持)するものは一切なくなります。すなわち、自由表面の法線方向には外力が作用していないので、力のつり合いから、自由端では境界面に垂直な方向の応力は常にゼロとなります。これは、すなわち、左から入射してきた圧縮の応力波による圧縮応力(-σ)と、反射に伴う応力波による引張応力(+σ)が足し合わされた結果、応力が0となることを意味します(図2の t=t2 の状態)。これはつまり、入射波と反射波の応力波の大きさが等しいということであり、固定端のときと同様、衝撃応力の大きさσと粒子速度Vの関係式(σ=-ρc0V )を考えると、粒子速度の大きさも等しいということになります。このことから、自由端では反射に伴う応力波は入射波と異なる符号を持つ同じ大きさの引張りの応力波であることが結論付けられることになります。更に、境界では伝播してきた圧縮の応力による右方向の粒子速度(+V)と反射した同じ大きさの引張りの応力による右方向の粒子速度(+V)の和となり、自由端での粒子速度の大きさは入射波の粒子速度の2倍(2V)となることも判ります。
なお、この例では入射応力が圧縮の場合について考えましたが、引張りの場合でも同様な議論が成り立つことを付記しておきます。
汎用非線形構造解析シミュレーションツールLS-DYNAについてはこちら http://www.engineering-eye.com/LS-DYNA/index.html