コラム:製造・構造
アプリケーションサービス部 CAEサービス第1課 津田 徹
[2019/10/25]
衝撃問題における応力波の伝播に特有な現象として、「固定端では同じ大きさの同符号の応力波が反射するのに対し、自由端では同じ大きさの異符号の応力波が反射する」ことが知られています。ではなぜ、境界条件の違いにより反射する応力波の符号が影響を受けてしまうのでしょうか? ここでは、皆さんの衝撃問題における理解の一助となるべく、この問題について1次元弾性波理論を用いて、不連続部における応力波の伝播と反射および透過の観点から説明してみたいと思います。
先ず、図1に示すような1次元衝撃問題における応力波は縦波(粗密波)であり、その大きさは次式で表されます。
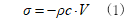
ここで、Vは粒子速度(衝撃速度とも呼ばれる)、ρは密度、cは応力波の伝播速度であり、衝撃応力σと粒子速度Vとは比例関係にあり、その比例定数ρcは縦衝撃における動的な変形抵抗で、音響インピーダンス(単にインピーダンスと呼ばれることもある)と呼ばれます。
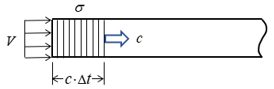
図1 衝撃速度と衝撃応力
また、このインピーダンス(=I)は、σに棒の断面積Aを乗じた力F(=A×σ)と速度Vとの比例定数として次式のように定義されることもあります。ここで、I=Aρc。
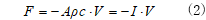
物質中を伝播する縦波の応力波には、引張力によって発生する場合は引張応力波(+符号)、圧縮力によって発生する場合は圧縮応力波(-符号)があり、この伝播速度cは伝播する材料のヤング率と密度によって決まり、1次元の場合は次式で求めることができます。
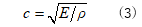
次に、応力波が図2に示すようなインピーダンスの変化する不連続面(棒①と棒②の境界)に到達して反射波と透過波に分かれる問題を考えます。棒①のインピーダンスとしてI1=A1ρ1c1、棒②のインピーダンスとしてI2=A2ρ2c2とします。
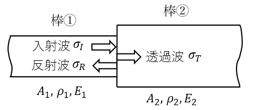
図2 不連続面における応力波の反射と透過
いま、大きさσIの応力波が棒①から棒②へ入射したとき、不連続面においてσRが反射し、σTが透過するものとします。このとき、不連続面における反射係数をα、透過係数をβとすると、反射波と透過波の大きさは次式で表すことができます。
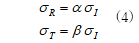
不連続面における力の釣り合いと粒子速度の連続の条件により次の関係式が成立します。
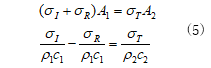
上式に式(4)を代入して反射係数αと透過係数βについて解けば、良く知られた次式が得られます。
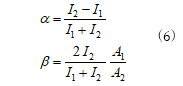
これより、以下のことが判ります。
更に、特別な場合として、自由端あるいは固定端における反射は次のようになります。
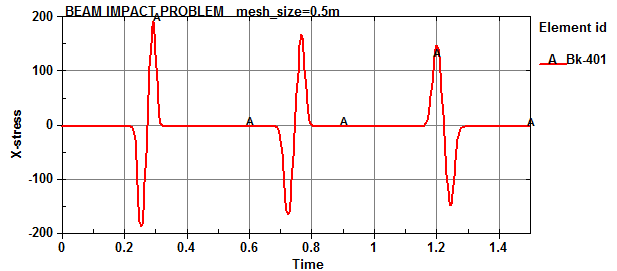
参考図A

参考図B

参考図C
・林卓夫,田中吉之助,衝撃工学,日刊工業新聞社
汎用非線形構造解析シミュレーションツールLS-DYNAについてはこちら http://www.engineering-eye.com/LS-DYNA/index.html