コラム:製造・構造
アプリケーションサービス部 CAEサービス1課 大場 一輝
[2018/04/13]
先日 (2017/12/4) 「CTCのAbaqusコア技術紹介セミナー」を開催させていただき、全5講演それぞれに対し大きな反響をいただくことができました。その中の1つとしてAbaqusの均質化プラグインを紹介させていただきました。
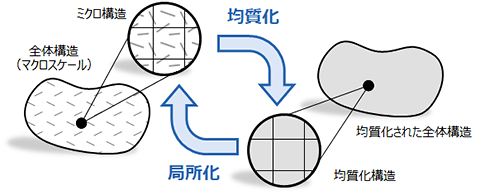
多くの材料はミクロレベルで観察すれば複数の相からなる複合構造(すなわちミクロ構造)を有していますが、大抵の場合こういったミクロ構造はマクロスケールの構造物全体に比較して微細であるため、ミクロ構造を無視して均質な材料であると仮定した際の等価物性を用いてモデル化することが普通です [1]。このミクロ構造とマクロ等価物性の関係に関する理論が均質化理論になります。下図は均質化理論のイメージ図で、ミクロ構造から等価物性を計算する均質化と、均質化された材料の状態(例えばひずみテンソル)からミクロ構造の状態(例えば応力分布)を計算する局所化に大きく分けることができます。
均質化法理論は最近注目を浴びている分野ですが、その起源は非常に古いものです。正確な起源を特定することは難しいですが、1957年のEshelbyによる等価介在物理論 [2] とそれに続く一連の平均場理論は間違いなく均質化法の重要な一手法であり、この時代から既に複合材を非均質材料とみなし、その力学特性をミクロ構造や各相の物性と関連付けて表現する試みが行われていたことが知られています。平均場理論は解析的な均質化手法であり、ミクロ構造(例えば楕円球形介在物に限定する等)やミクロ各相の材料物性(大半は等方性弾性体に限定)にかなり厳しい制約があるものの、理論計算式により等価マクロ材料特性を抽出することが可能です。また母材と介在物の体積分率のような最低限の情報から均質化物性の上下界を得る研究はもっと古く、19世紀末のVoigtの研究 [3] や20世紀前半のReussによる研究 [4] が知られています。
一方、後年になって、より汎用的な構造に対して均質化を適用するための数値解析的な均質化理論(数学的均質化法)が考案されました [5-7]。こちらは有限要素法により離散化・実装される場合が大半で、ミクロ構造はメッシュで直接モデリングできればよく、材料特性は有限要素法の材料モデルとして表現できればよいため、前述の平均場理論や上下界理論に比べ適用対象がはるかに広いものとなります。なお、Abaqusの均質化プラグインはこちらの数学的均質化理論を実装したツールキットであり、有限要素法ソルバーとしてAbaqus/ Standardを利用し、必要な境界条件設定やポスト処理等をツールキットにて簡単に行えるようになっています。
全ての均質化理論に共通していることは、冒頭で触れた通りミクロスケールとマクロスケールの橋渡しをしているという、均質化理論の本質的な特徴です。多くの場合、有限要素法解析等で利用する材料物性は材料試験により、材料のミクロ構造を無視する形でマクロ物性を直接計測します。これに対し、均質化理論を使えばミクロ構造やミクロ各相の材料物性がマクロスケールの等価物性に与える影響を定量的に議論することが可能になります。近年では解析の高精度化の要求が高まる中で、マクロスケールの現象論的な材料モデルをより理論的に紐解くためにミクロスケールでの挙動および現象の理解に注目が集まっており、ミクロとマクロの橋渡しをする均質化法も、マルチスケール解析の根幹をなす手法として近年その存在感を強めつつあります。
先日のセミナーではAbaqus均質化法プラグインを紹介しましたが、CTCでは他にもいくつか均質化法ソフトウェアを核としたマルチスケール解析ソリューションをご提供しております。後半の記事ではその中から
の2つをご紹介させていただきます。合わせてお読みいただければと思います。
均質化法計算ソフトウェア MICRESS HOMATの紹介ページはこちら http://www.engineering-eye.com/HOMAT/index.html
複合材料解析システムComposites Dreamに関する詳しい情報はこちら http://www.engineering-eye.com/COMPOSITES_DREAM/index.html